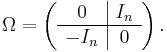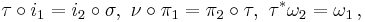Symplectic manifold

In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology. Symplectic manifolds arise naturally in abstract formulations of classical mechanics and analytical mechanics as the cotangent bundles of manifolds, e.g., in the Hamiltonian formulation of classical mechanics, which provides one of the major motivations for the field: The set of all possible configurations of a system is modelled as a manifold, and this manifold's cotangent bundle describes the phase space of the system.

Any real-valued differentiable function, H, on a symplectic manifold can serve as an energy function or Hamiltonian. Associated to any Hamiltonian is a Hamiltonian vector field; the integral curves of the Hamiltonian vector field are solutions to Hamilton's equations. The Hamiltonian vector field defines a flow on the symplectic manifold, called a Hamiltonian flow or symplectomorphism. By Liouville's theorem, Hamiltonian flows preserve the volume form on the phase space.

1 Definition
2 Linear symplectic manifold
3 Lagrangian and other submanifolds
4 Lagrangian fibration
5 Lagrangian mapping
6 Special cases and generalizations
7 See also
8 Notes
9 References
10 External links

Definition

A symplectic form on a manifold M is a closed non-degenerate differential 2-form ω.^[1]^[2] The non-degeneracy condition means that for all p ∈ M we have the property that there does not exist non-zero X ∈ T_pM such that ω(X,Y) = 0 for all Y ∈ T_pM. The skew-symmetric condition (inherent in the definition of differential 2-form) means that for all p ∈ M we have ω(X,Y) = −ω(Y,X) for all X,Y ∈ T_pM. Recall that in odd dimensions antisymmetric matrices are not invertible. Since ω is a differential two-form the skew-symmetric condition implies that M has even dimension.^[1]^[2] The closed condition means that the exterior derivative of ω, namely dω, is identically zero. A symplectic manifold consists a pair (M,ω), of a manifold M and a symplectic form ω. Assigning a symplectic form ω to a manifold M is referred to as giving M a symplectic structure.

Linear symplectic manifold

There is a standard linear model, namely a symplectic vector space R²ⁿ. Let R²ⁿ have the basis {v₁, ... ,v_2n}. Then we define our symplectic form ω so that for all 1 ≤ i ≤ n we have ω(v_i,v_n+i) = 1, ω(v_n+i,v_i) = −1, and ω is zero for all other pairs of basis vectors. In this case the symplectic form reduces to a simple quadratic form. If I_n denotes the n × n identity matrix then the matrix, Ω, of this quadratic form is given by the (2n × 2n) block matrix:

$\Omega = \left(\begin{array}{c|c} 0 & I_n \\ \hline -I_n & 0 \end{array}\right).$

Lagrangian and other submanifolds

There are several natural geometric notions of submanifold of a symplectic manifold.

symplectic submanifolds (potentially of any even dimension) are submanifolds where the symplectic form is required to induce a symplectic form on them.
isotropic submanifolds are submanifolds where the symplectic form restricts to zero, i.e. each tangent space is an isotropic subspace of the ambient manifold's tangent space. Similarly, if each tangent subspace to a submanifold is co-isotropic (the dual of an isotropic subspace), the submanifold is called co-isotropic.

The most important case of the isotropic submanifolds is that of Lagrangian submanifolds. A Lagrangian submanifold is, by definition, an isotropic submanifold of maximal dimension, namely half the dimension of the ambient symplectic manifold. Lagrangian submanifolds arise naturally in many physical and geometric situations. One major example is that the graph of a symplectomorphism in the product symplectic manifold (M × M, ω × −ω) is Lagrangian. Their intersections display rigidity properties not possessed by smooth manifolds; the Arnold conjecture gives the sum of the submanifold's Betti numbers as a lower bound for the number of self intersections of a smooth Lagrangian submanifold, rather than the Euler characteristic in the smooth case.

Lagrangian submanifolds arise naturally in many physical and geometric situations. We shall see below that caustics can be explained in terms of Lagrangian submanifolds.

Lagrangian fibration

A Lagrangian fibration of a symplectic manifold M is a fibration where all of the fibres are Lagrangian submanifolds. Since M is even dimensional we can take local coordinates (p₁,…,p_n,q₁,…,q_n), and by Darboux's theorem the symplectic form ω can be, at least locally, written as ω = ∑ dp_k ∧ dq_k, where d denotes the exterior derivative and ∧ denotes the exterior product. Using this set-up we can locally think of M as being the cotangent bundle T*Rⁿ, and the Lagrangian fibration as the trivial fibration π : T*Rⁿ ↠ Rⁿ. This is the canonical picture.

Lagrangian mapping

Let L be a Lagrangian submanifold of a symplectic manifold (K,ω) given by an immersion i : L ↪ K (i is called a Lagrangian immersion). Let π : K ↠ B give a Lagrangian fibration of K. The composite (π ○ i) : L ↪ K ↠ B is a Lagrangian mapping. The critical value set of π ○ i is called a caustic.

Two Lagrangian maps (π₁ ○ i₁) : L₁ ↪ K₁ ↠ B₁ and (π₂ ○ i₂) : L₂ ↪ K₂ ↠ B₂ are called Lagrangian equivalent if there exist diffeomorphisms σ, τ and ν such that both sides of the diagram given on the right commute, and τ preserves the symplectic form.^[2] Symbolically:

$\tau \circ i_1 = i_2 \circ \sigma, \ \nu \circ \pi_1 = \pi_2 \circ \tau, \ \tau^*\omega_2 = \omega_1 \, ,$

where τ*ω₂ denotes the pull back of ω₂ by τ.

Special cases and generalizations

A symplectic manifold endowed with a metric that is compatible with the symplectic form is an almost Kähler manifold in the sense that the tangent bundle has an almost complex structure, but this need not be integrable. Symplectic manifolds are special cases of a Poisson manifold. The definition of a symplectic manifold requires that the symplectic form be non-degenerate everywhere, but if this condition is violated, the manifold may still be a Poisson manifold.

A multisymplectic manifold of degree k is a manifold equipped with a closed nondegenerate k-form. See F. Cantrijn, L. A. Ibort and M. de León, J. Austral. Math. Soc. Ser. A 66 (1999), no. 3, 303-330.

A polysymplectic manifold is a Legendre bundle provided with a polysymplectic tangent-valued $(n%2B2)$ -form; it is utilized in Hamiltonian field theory. See: G. Giachetta, L. Mangiarotti and G. Sardanashvily, Covariant Hamiltonian equations for field theory, Journal of Physics A32 (1999) 6629-6642; arXiv: hep-th/9904062.

Notes

^ ^a ^b Maurice de Gosson: Symplectic Geometry and Quantum Mechanics (2006) Birkhäuser Verlag, Basel ISBN 3-7643-7574-1. (page 10)
^ ^a ^b ^c Arnold, V. I.; Varchenko, A. N.; Gusein-Zade, S. M. (1985). The Classification of Critical Points, Caustics and Wave Fronts: Singularities of Differentiable Maps, Vol 1. Birkhäuser. ISBN 0817631879

References

Dusa McDuff and D. Salamon: Introduction to Symplectic Topology (1998) Oxford Mathematical Monographs, ISBN 0-19-850451-9.
Ralph Abraham and Jerrold E. Marsden, Foundations of Mechanics, (1978) Benjamin-Cummings, London ISBN 0-8053-0102-X See section 3.2.
Maurice de Gosson: Symplectic Geometry and Quantum Mechanics (2006) Birkhäuser Verlag, Basel ISBN 3-7643-7574-1.
Alan Weinstein (1971). "Symplectic manifolds and their lagrangian submanifolds". Adv Math 6 (3): 329–46. doi:10.1016/0001-8708(71)90020-X.

External links

Ü. Lumiste (2001), "Symplectic Structure", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=s/s091860
Sardanashvily, G., Fibre bundles, jet manifolds and Lagrangian theory. Lectures for theoreticians,arXiv: 0908.1886
Examples of symplectic manifolds on PlanetMath